[bocsánat a címért, mert egy lopás: egy szegedi kémikusnak volt ilyesmi címmel elõadássorozata ...]

Mostanság olvastam egy cikket a fizikusok kedvenc pornószájtján amit meg akarok osztani veletek, óh Mindenki, aki erre vette böngészõje útját.

Olvasó! A mai mese a Rayleigh–Taylor instabilitás apropólán a színes fizika világába kíván bevezetni (azahogy hogyan lettem én a fizika barátja a szememen keresztül)

A Rayleigh–Taylor instabilitással én elõször akkor találkoztam mikor már "répa, retek, mogyorót nem "lépa, letek, mogyoló"-nak mondtam, de éppen hogy csak nem ...

Volt egy nagy lavorunk, amiben mindenfele fizikai kísérletet csináltam (prizmát egy tükör segedelmével, például) és akkor találtam rá - édesanyám õszinte bánatára -  a tintára!

A tollbetéteket csípõfogóval kettévágni, és az "eleven" tintatól lucskos végét a tollbetétnek belemartani a vízbe! Határtalanul változatos, ugyanakkor jól tipizálható formák jonnek ki

(természetesen édesanyám kifogása az volt, hogy az így bugyogó tinta az galád módon mindenhová került: földre, kezemre, ruhámra, aztán a ruhám valahogy valamiféle gyûjtõhellyé vált, mivel a kezemrõl is elõbb-utóbb a ruhámra került ... csupa meglepetés az élet ...)

Szóval ez volt az elsõ élményem a Rayleigh–Taylor instabilitással, habár a két úriember nevével még nem találkoztam, az "instabilitás" szót meg hóttuti, hogy nem tudtam volna kimondani.

Aztán az egyetemen megtudtam, hogy ha van két folyadékunk különbözõ sûrûséggel, és a nagyobb sûrûségû felül van, akkor a határukon kialakul egy instabil állapot, ott az egyik folyadékréteg lefelé, a másik felfelé kezd el; mozogni és egy nagyon bonyolult mintázat alakul ki. De valahogy ez a mozgás "optimalizálva" lesz, miszerint egymástól elkülönölõ régiókban fog a folyadék le- és felfele mozogni.

A képen (számítógépes modell-számítás) a piros dolgok éppen felfelé mozognak, a kékek meg lefelé.

Az fenn említett cikk is egy ilyenfajta mintázatképzõdést figyelt meg egy nagyon hetköznapi rendszerben (ahol már minannyian megfigyelhettük azt, habár nem tudtuk nevén nevezni): a kávénál mikor tej keveredik beléje. No Õk csavartak egyet a rendszeren és a kávé keveredését tejben vizsgálták.

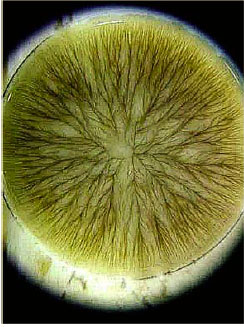Gyönyörû ("szép vagy mintázat, legalább nekem szép") mintázatokat fényképeztek,de ez nem lenne elég egy tudományos cikkhez (merthát ez egy tudományos cikk szeretne lenni, habár szép, és hát sok ember szemáben ami tudományos, az száraz! ... de legalább is nem szép ... a szép hagyományos értelmében ... pedig nem is ...), és hát belevontak a dologba egy másik vizuálisan is élvezhetõ dolgot: a Sierpinski szivacsot ...

Az igazság az, hogy Sierpinski nevével elõször egy számítógépes képernyõvédõ nevével kapcsolatban találkoztam. Azonnal megértettem, hogy mirõl van szó (valószínûsítem, hogy én a lassabb "azonnal megértettem"-hez tartoztam ...) hiszen a szabály egyszerû: végy egy háromszöget (négyszöget),, vágdd szét 4 (9) egynlõ részre, vedd ki a középsõt, és alkalmazd a ugyanezt a szabalyt a megmaradt 3 (8) háromszögön (négyszögön) ... Ugye milyen egyszerû? De csinálni még ennél is egyszerûbb.

Az ilyen "önhasonló" (merhogy a fent leírt szbályt végtelenszer ismételve barmely kis négyszögre "rázoomolva" az eredeti ábrához teljesen hasonlót kapunk) mintáknak  (avagy más szóval fraktáloknak) azon tulajdonságát, hogy mennyire képesek "kitölteni a teret" a fraktáldimenzió nevû mértékegységgel szokás leírni.

A nem gyakorlott szemûeknek el kell mondani, (és nekik ezt utána be kell látni), hogy az elõzõ kávé-mintázat is önhasonló (azaz fraktál) (ha ez sikerul, akkor rájövünk, hogy az élet tele van fraktálokkal (1, 2, 3).

Ha ez sikerült, akkor jön a meglepetés!

A négyzetalapú Sierpinski szivacs és a kávé-mintázat fraktáldimenziója megegyezik!

Ebbõl (és néhány egyébb hasonló kvantitatív (számokkal laírható) egyezésbõl) a kutatók azt a következtetest vontak le, hogy a kialakulasi mechanizmus ugyanaz lehet a két esetben.

Vége! Nem írják, hogy mi ez a mechanizmus (bár a Sierpinski szivacs kialakulását tudjuk ...).

Kár! De legalább apropót szolgáltatott néhány száp dolog megemlítésére.

Aludjatok jól, és ne keljetek fel riadtan, ha Rayleigh–Taylor instabilitási mintazattal vagy Sierpinski szivaccsal álmodtok.

k.